Zugversuch ISO 6892 - Wissen
Zugfestigkeit Dehnung Streckgrenze ... einfach erklärt
Wirklich alles, was hergestellt wird, muss (sollte) geprüft werden, damit der Werkstoff beziehungsweise das Produkt die zugedachte Aufgabe erfüllen kann. Das kann die Lasche einer Getränkedose sein, die reißt, ohne dass die Dose geöffnet wird, oder eine Fahrzeugkarosserie die zur “Banane” wird weil der verwendete Stahl mangelhaft war. Dies gilt für alle Werkstoffe: Kunststoff, Klebstoff, Glas und vor allem für Metall. Denn sobald ein Produkt Kräften standhalten muss, ist dies in der Regel Stahl der Werkstoff, der diese Aufgabe am besten erfüllt. Dabei ist NICHT die Zugfestigkeit (maximale Kraft geteilt durch den Querschnitt der Probe) der wichtigste Kennwert sondern die Schädigungsgrenze ReH (Streckgrenze) beziehungsweise die Ersatz-Streckgrenze = Dehngrenze Rp0,2.
Hier finden Sie Infos zum Unterschied zwischen Reh und Rp0,2, weiteren Materialkennwerten und über eine für den Zugversuch erforderliche Zugprüfmaschine.
WISSENSWERTES
Die Anforderungen an Metalle sind sehr unterschiedlich, teilweise extrem. Metalle für Stahlfedern müssen extrem fest / hart und trotzdem elastisch / federnd sein. Hingegen erfordert die Fertigung von z. B. Kochtöpfen, dass eine plane Blechronde extrem umgeformt wird (Tiefziehen = Material-Dehnung) ohne das eine Ausdünnung oder ein Riss entsteht.
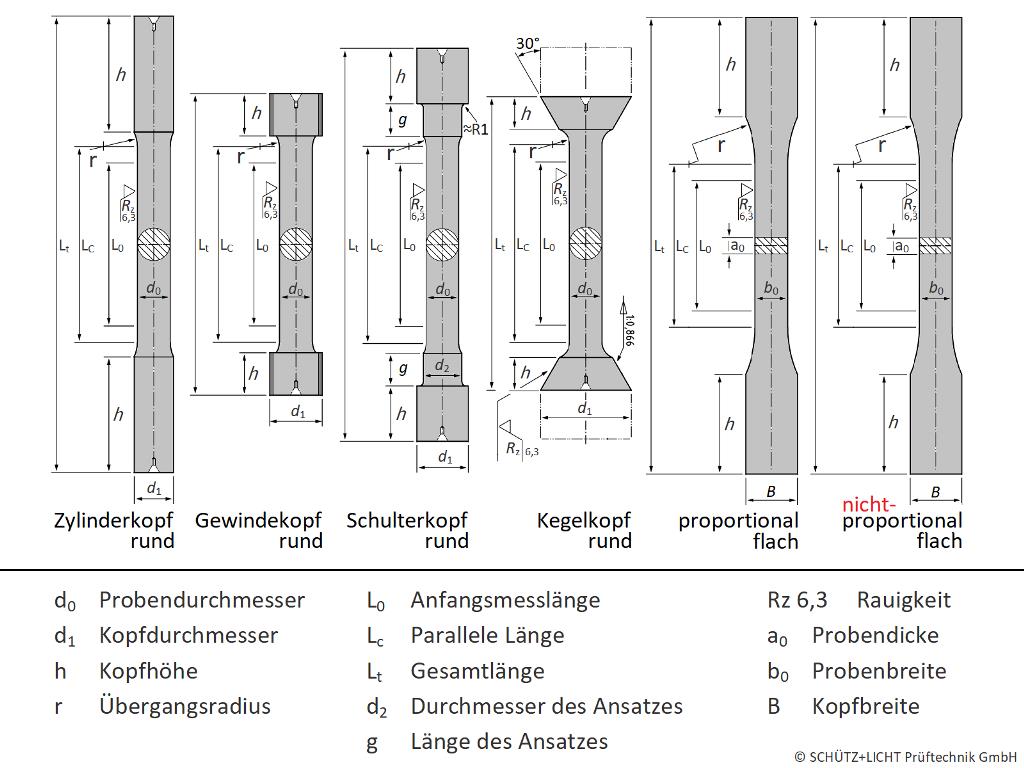
Um fertigungsbedingte Qualitäts-Schwankungen auszuschließen werden Metall-Zwischenprodukte regelmäßig mittels einem Zugversuch auf einer Zugprüfmaschine geprüft. Die Stangen, Rohre, Bleche erfordern die Fertigung unterschiedlicher Zugproben: Zylinderkopf, Gewindekopf oder Blech-Flachprobe.
Die wichigsten mechanisch technologischen Material-Kennwerte eines Metall- Zugversuch sind:
* Elastizitäts-Modul / Hilfslinie Hookesche Gerade
* Streckgrenze ReH / Dehngrenze Rp0,2
* Zugfestigkeit Rm
* Lüders-, Gleichmaß-, Bruch- Dehnung A5,65/A80
* Einschnürung Z
WISSENSWERTES
Die Anforderungen an Metalle sind sehr unterschiedlich, teilweise extrem. Metalle für Stahlfedern müssen extrem fest / hart und trotzdem elastisch / federnd sein. Hingegen erfordert die Fertigung von z. B. Kochtöpfen, dass eine plane Blechronde extrem umgeformt wird (Tiefziehen = Material-Dehnung) ohne das eine Ausdünnung oder ein Riss entsteht.
Um fertigungsbedingte Qualitäts-Schwankungen auszuschließen werden Metall-Zwischenprodukte regelmäßig mittels einem Zugversuch auf einer Zugprüfmaschine geprüft. Die Stangen, Rohre, Bleche erfordern die Fertigung unterschiedlicher Zugproben: Zylinderkopf, Gewindekopf oder Blech-Flachprobe.
Die wichigsten mechanisch technologischen Material-Kennwerte eines Metall- Zugversuch sind:
* Elastizitäts-Modul / Hilfslinie Hookesche Gerade
* Streckgrenze ReH / Dehngrenze Rp0,2
* Zugfestigkeit Rm
* Lüders-, Gleichmaß-, Bruch- Dehnung A5,65/A80
* Einschnürung Z
Die Anforderungen an Metalle sind sehr unterschiedlich, teilweise extrem. Metalle für Stahlfedern müssen extrem fest / hart (hohe Zugfestigkeit) und trotzdem elastisch / federnd (elastische Dehnung) sein. Hingegen erfordert die Fertigung von z. B. Kochtöpfen, dass eine plane Blechronde extrem umgeformt wird (Tiefziehen = Materialumformung bzw. plastische Dehnung) ohne das eine Ausdünnung oder ein Riss entsteht.
Um fertigungsbedingte Qualitäts-Schwankungen auszuschließen werden Metall-Zwischenprodukte regelmäßig mittels Zugversuch auf einer Zugprüfmaschine geprüft. Die Stangen, Rohre, Bleche erfordern die Fertigung unterschiedlicher Zugproben mit Zylinderkopf, Gewindekopf oder Blech-Flachprobe.
Ablauf der Prüfung
Der Zugversuch gemäß ISO 6892 erfolgt klassisch in drei Phasen:
1. Verlängerung der Zugprobe bei geringer Geschwindigkeit im elastischen Bereich
Elastische, reversible Dehnung
2. Konstante Kriechgeschwindigkeit zw. elastischer und plastischer Dehnung
Erste Schädigung: Streckgrenze ReH / Dehngrenze Rp0,2
3. Deutliche Erhöhung der Geschwindigkeit im plastischen Bereich bis zum Bruch
Irreversible Dehnung
Für einen Zugversuch ISO6892 erforderlich:
Prüfsoftware
Metallzugversuch

Prüfzeugnis Zugversuch Metall
Dehnungsmesser
Klasse 1 gemäß ISO9513

Extensometer MFX
Spannzeug
je nach Probenform

Spannzeug für Gewindekopfproben
Was passiert bei der Streckgrenze ReH?
Die erste Schädigung des Metalls
Wichtiger als die Zugfestigkeit ist die Streckgrenze ReH (oder Dehngrenze Rp0,2): Sobald Metall dauerhaft verformt wird, ist dies der "Anfang vom Ende".
Niedrig- oder unlegiertes Eisen hat eine Streckgrenze ReH. Wenn es im Zugversuch gedehnt wird, tritt bei einer Kraft bzw. der zu bestimmenden Spannung ein spontanes Nachgeben auf. Die am höchsten belasteten Kraftverbände der „verhakten“ Metallkristalle rutschen ab und es kommt zu einem deutlich sichtbaren Spannungsabfall . Danach lassen andere „Kletthaken“ einen erneuten Kraftanstieg zu, bis auch diese versagen und abrutschen. Sind alle groben Verhakungen abgerutscht, verschwindet der Effekt und alle Kristalle werden gemeinsam bis zum Bruch der Probe gedehnt.
Wozu dient die Dehngrenze Rp0,2?
Wird Eisen legiert (Chrom-, Mangan-Beimischung u. a.) entsteht Stahl. Damit einhergehend entstehen feinere Kristallgefüge. Hierdurch und durch Kaltumformung (walzen, hämmern) oder Wärmebehandlungen wird der Lüders-Effekt unterdrückt.
Statt der einfach auswertbaren Streckgrenze ReH muss das E-Modul und parallel dazu die „Ersatz-Streckgrenze“ ermittelt werden. Dazu wird parallel zur Hookeschen Geraden die plastische Dehngrenze Rp0,2% ausgewertet.
Zugversuch - Bestandteil der Qualitätssicherung
Werkstoffe und Materialien können in der Industrie heute mit hoher Exaktheit auf die gewünschte Materialgüte hin produziert werden. Trotzdem muss der Prozess der Materialerzeugung und der Weiterbehandlung bis hin zum fertigen Endprodukt (Material - nicht Bauteil) ständig überwacht werden, da verschiedenste Faktoren die Qualität stark beeinflussen können. So ist z. B. in der Stahlindustrie in der flüssigen Phase des Roheisens / Rohstahls die Zusammensetzung der Legierung fast einziges Kriterium. Hier wird z. B. eine Spektralanalyse verwendet um die verschiedenen Elemente bis hin zu Spurenelementen bestimmen zu können. Bei der Weiterverarbeitung kommt es aber durch die verschiedensten Verfahren teilweise zu extremen Beeinflussungen des Materials. Die Eigenschaften des Materials können durch verschiedenste Behandlungsmethoden extrem verändert werden. Als Beispiel sind hier einige wenige Bearbeitungsverfahren genannt:
- Walzen des Stahls zur Form- / Dickenänderung - Verdichtung des Materials = höhere Zugfestigkeit und Härte, geringere Dehnfähigkeit
- Härtung des Stahls - Gefügeveränderung = höhere Zugfestigkeit und Härte, geringere Dehnfähigkeit, Versprödung
- Verzinkung - Materialauftrag = verhindert rosten, die chemische Behandlung in mehreren Schritten kann zu Versprödungen führen
- Zwischenglühen - Gefüge entspannt sich = Zugfestigkeit + Härte verringern sich, Dehnfähigkeit steigt, Versprödung sinkt
- Strahlen des Materials (mit Stahlkugel, Keramikkugeln, Sand) - Materialabtrag (Rost) / Oberflächenverdichtung = Zugfestigkeit / Härte an der Oberfläche steigt
Durch eine Vielzahl weiterer Behandlungs- und Verarbeitungsschritte können sich die Materialeigenschaften dramatisch ändern. Wenn aber die Konstruktion eines Bauteils oder z. B. einer Brücke die Verwendung eines Stahls mit einer Festigkeit von 800 MPa vorsieht, dann muss auch geprüft werden, dass diese Anforderung erfüllt wird. Ein Versagen des Bauteils muss ausgeschlossen sein (Brückenbau, Fahrzeugkarosserien, Kräne und alle Baugruppen und Komponenten die statische oder dynamische Lasten aufnehmen muss).
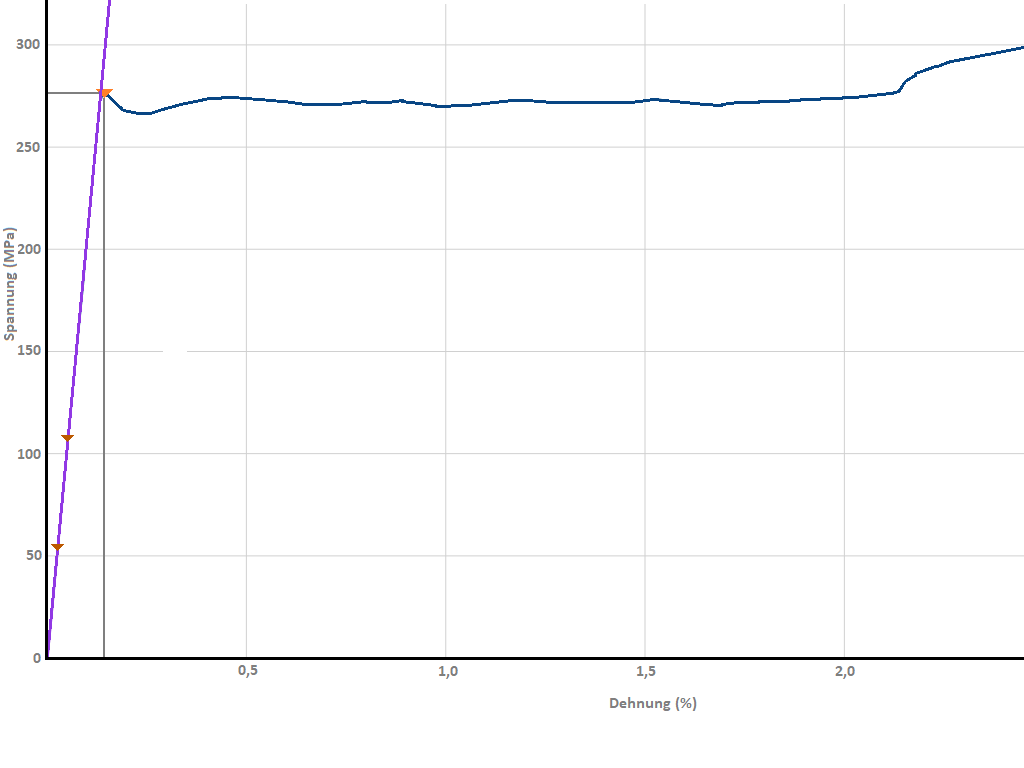
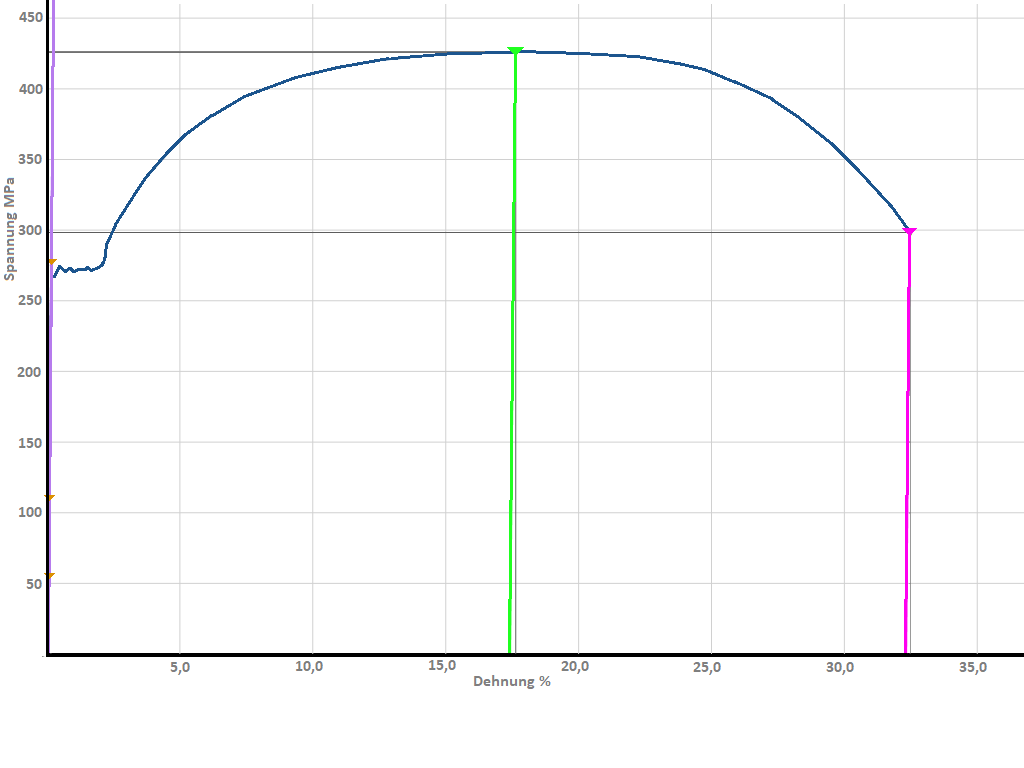
Hier Diagramme die den Unterschied zwischen einer Streckgrenze und einer Dehngrenze darstellen (links: Diagramme mit Streckgrenze / rechts: Diagramme mit einer Dehngrenze)
Ermittlung Materialeigenschaften metallischer Werkstoffe
Es gibt nicht grundsätzlich "gutes" oder "schlechtes" Metall sondern der Einsatzzweck / Kosten bestimmen die Anforderungen an den Werkstoff. Z. B. muss ein Stahl für ein Ventil in einem Verbrennungsmotor extrem hochfest und hart sein, damit ein vorzeitiger Verschleiß verhindert wird. Hingegen muss ein Blech für einen Autokotflügel relativ weich sein, damit die Umformung ohne Risse / Bruch des Materials erfolgen kann (Tiefziehprozess).
Die Materialeigenschaften werden u. a. dadurch ermittelt, dass eine Zugprobe mittels Metallzugversuch geprüft wird. Am häufigsten werden diese Versuche in der Stahlindustrie, Kunststoffindustrie und Gummiindustrie durchgeführt (und einige mehr).
Je nach Verwendungsart werden die Produkte (Basismaterialien) in verschiedenen Geometrien verarbeitet (Rohre, Stangen, Brammen, Bleche und natürlich auch ganze Bauteile). Somit sind verschiedenste Probenformen erforderlich um die Materialkenndaten ermitteln zu können. Besitzt das Produkt ein großes Volumen so wird in der Stahlindustrie in vielen Fällen aus dem Vollmaterial eine Zugprobe mit einem runden Querschnitt hergestellt (Drehbank). Andere Produkte (z. B. Bleche) erfordern es, dass eine Flachzugprobe mit quadratischem oder rechteckigem Querschnitt hergestellt und geprüft wird.
Damit die Ergebnisse unabhängig vom Querschnitt miteinander verglichen werden können werden alle Messwerte auf eine Vergleichsgeometrie bezogen. Dies ist in der Regel mm² für die Festigkeit bzw. eine Bezugslänge L0 (Länge Null - Fachbegriff: Ausgangsmesslänge) für die Dehnung. So wird z. B. die Zugfestigkeit (Kurzzeichen Rm) in der Einheit N/mm² (Newton per mm²) bzw. gem. ISO 6892 in MPa ausgewiesen (Mega-Pascal = Umrechnungsfaktor 1:1 zu Newton mm²).
Bei einem
Kunststoff liegt die Zugfestigkeit bei z. B. 20 MPa (zur Veranschaulichung: ~ 2 kgf Gewichtskraft je mm²)
weichen Blech (Autokotflügel) bei 200 MPa (zur Veranschaulichung: ~ 20 kgf Gewichtskraft je mm²)
hochfester Federstahl bei 2.100 MPa (zur Veranschaulichung: ~ 210 kgf Gewichtskraft je mm²)
Um diese Einheit werten zu können sei für den "Normalbürger" an dieser Stelle zur Veranschaulichung gesagt:
1000 MPa entsprechen etwa 100 kgf Gewichtskraft (ca. 101,93 kg - Divisor 9,807)
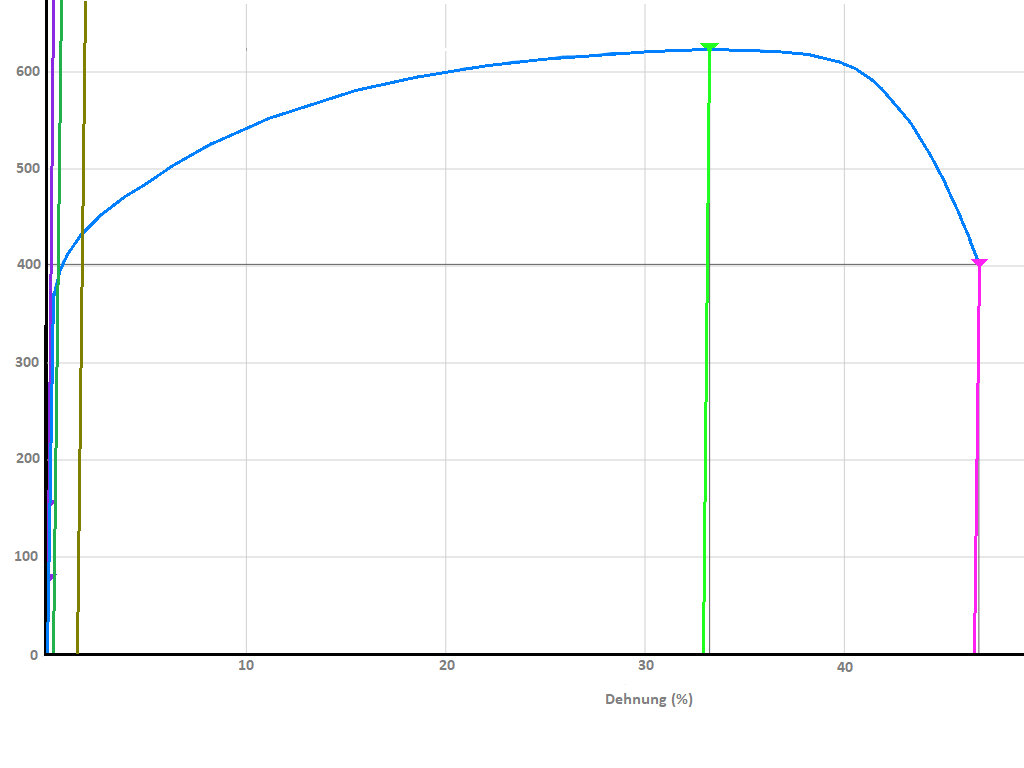
Wenn man einen eckigen Draht mit einem Querschnitt von 1 x 1 mm = 1 mm² mit einer Kraft von 1000 Newton (bezogen auf 1 mm² = 1000 MPa) bzw. 101,93 kg belastet wird dieser gedehnt und bricht. Der Prüfling wird in ein Spannzeug eingespannt und mit sehr langsamer, stetig steigender Verlängerung beaufschlagt. Die Aufzeichnung des Versuchs erfolgt heute auf elektronischer Basis in Form eines Diagramms. Bei heutigen elektronischen Auswertesystemen dient das Diagramm jedoch nur noch der visuellen Kontrolle und Darstellung des Versuchsverlaufs. Die Kennwerte werden anhand komplexer Algorithmen ermittelt. Die Diagrammdarstellung und die Ergebnisse sollen und müssen jedoch annähernd deckungsgleich sein, um dem Anwender einen Vergleich zwischen Messwert <-> Diagramm zu liefern um eine visuelle Beurteilung zu ermöglichen.
Grundsätzliches zu den nachfolgenden Diagrammen
Kenndaten mit R (Spannungswerte σ) kennzeichnen die aktuell an diesem Punkt anstehende Kraft geteilt durch die Anfangs-Querschnittsfläche (S0) der Probe - im Diagramm auf der vertikalen Achse dargestellt / "abgelesen".
Kenndaten mit A (Dehnungswerte ε) kennzeichnen die aktuell an diesem Punkt anstehende Verlängerung (Dehnung) des Prüflings bezogen auf eine Ausgangsbasis (L0 - Anfangsmesslänge) - im Diagramm auf der horizontalen Achse des Graphen dargestellt / "abgelesen"
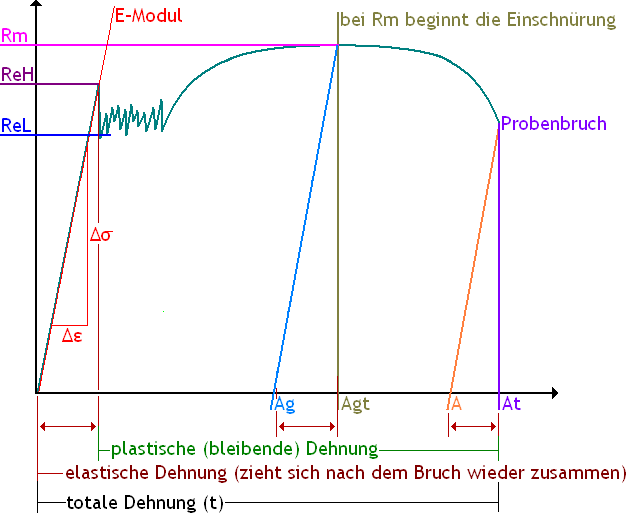
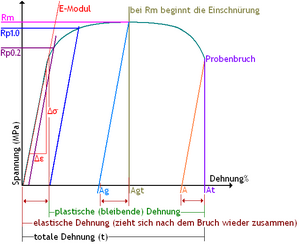
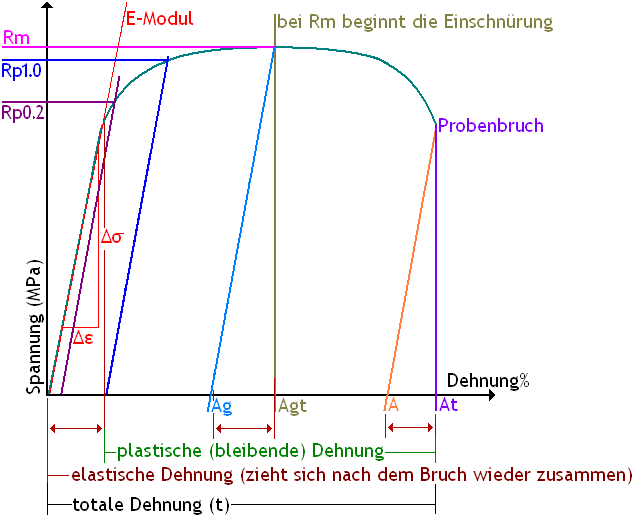
Die einfachste Form der Erklärung ist meist die Darstellung anhand von Skizzen. Nachfolgend eine Skizze eines Graphen Streckgrenzen-Material
Erklärung der Werkstoffkenndaten
- ReH - Obere Streckgrenze
Wird der Prüfling weiterbelastet, so erfolgt eine erste Schädigung: Kräfteverbünde im Material versagen (vereinfacht: Fasern reißen) und es kommt zum spontanen Kraftabfall (bzw. Spannungsabfall). Dieser höchste Punkt auf der Geraden wird als ReH bezeichnet. Nach dieser ersten Schädigung verlängert sich die Probe irreversibel - bleibend verlängert. Bis zu dem Kennwerte ReH könnte der Konstrukteur einen Werkstoff (Bauteil) belasten ohne dass dieser bleibend geschädigt wird. Natürlich bleibt der Konstrukteur zur Sicherheit deutlich von diesem Punkt entfernt.
- ReL - Untere Streckgrenze
Nachdem die erste Schädigung des Materials erfolgte (ReH) fällt die Kraft / Spannung (je nach Material) sehr deutlich. Dies erfolgt teilweise auf einen deutlich niedrigeren Wert als dies für die Lüders-Dehnung üblich ist. Den ersten (sehr tiefen) Abfall der Spannung nennt man Einschwingverhalten (extremer Ausschlag der Kurve nach unten direkt nach ReH). Dieser Ausschlag bleibt für den Kennwert ReL unbeachtet. Im nun folgenden Lüders-Bereich wird der unterste Ausschlag des Graphen gesucht. Dieser Punkt wird als untere Streckgrenze bezeichnet und ergibt den Punkt auf den die Spannung maximal abfällt bevor im weiteren Verlauf ein erneuter stetiger Anstieg der Spannung erfolgt.
- Verfestigung des Materials (stetiger Anstieg nach der Lüders-Dehnung)
Nachdem alle "problematischen" Kräfteverbünde gerissen sind (Lüders-Dehnung abgeschlossen) steigt die Spannung erneut und stetig an. Dies kann man etwas so erklären: Einzelne Fasern in einem Seil waren zu kurz. Diese sind nun gerissen (Lüders-Verhalten). Nachdem nun alle "zu kurzen Fasern" gerissen sind übernehmen nun wieder alle Fasern eines Seils die Last - die Spannung steigt stetig erneut an (ohne das weitere einzelne Fasern reißen).
- Rm - Zugfestigkeit
Nachdem die Spannung stetig weiter angestiegen ist kommt es zu einem Zustand bei dem keine weitere Kraftsteigerung erforderlich ist um die Zugprobe zu verlängern: Das Material dehnt sich gleichmäßig weiter bis das an einer Stelle eine (anfangs geringe) Einschnürung (Taillenbildung) des Prüflings beginnt. Der höchste Punkt der Kraft (Spannung) wird ermittelt und die Zugspannung ermittelt (Maximale Kraft durch Probenquerschnitt = Rm in N/mm² bzw. richtiger MPa). Nach Überschreitung der maximalen Kraft beginnt sich die Probe an einer Stelle einzuschnüren. Diese Einschnürung erfolgt nun immer schneller bis das der Prüfling bricht und zweigeteilt ist.
- Lüders - Dehnung Ae (im Diagramm nicht mit einem Kennbuchstaben eingezeichnet)
Im nun folgenden Teil des Zugversuchs passieren diese Spannungsabfälle (je nach Materialeigenschaft) unterschiedlich oft: Es entsteht eine Oszillations-Kurve die nach seinem Entdecker als Lüders-Dehnung bezeichnet wird. Dabei rutschen die Kristalle / Kräfteverbünde aneinander vorbei (Spannungsabfall) und verhaken sich erneut (Spannungsanstieg). Am einfachsten kann man sich das vorstellen wie die einzelnen Fasern einen wenn man die Fasern eines Seils (unten mehr).
- Elastische Dehnung (Verlängerung der Probe bis ReH)
- Plastische Dehnung (Verlängerung der Probe nach ReH bzw. nach Verlassen der Geraden)
Sobald die Streckgrenze ReH überschritten ist bzw. die gerade Linie der Elastizität verlassen wird beginnt die bleibende plastische Dehnung. Die Probe wird bleibend verlängert und kehrt nicht mehr zur Ausgangslänge zurück auch wenn die Kraft gänzlich entlastet wird.
- Bruchdehnung A
Ist die bleibende Dehnung die die Probe bis zum Bruch erfährt. Sobald die Probe bricht zieht sich der elastische Anteil wieder zusammen und verkürzt die Probe etwas (typisch 0,3%).
- Totale Bruchdehnung At
Ist die bleibende Dehnung die die Probe bis zum Bruch erfährt zuzüglich des elastischen Anteils. Diese Dehnung kann nur dann gemessen werden wenn ein Dehnungsmesser die Verlängerung der Probe (bleibende Dehnung inklusive elastischem Anteil) bis zum Bruch aufzeichnet.
- Gleichmaßdehnung Ag
Die normgerechte Zugprobe dehnt sich in dem parallelen Bereich des Querschnitts gleichmäßig. Üblicherweise besitzt eine normgerechte Zugprobe eine Hantelform (Knochenform). Die Gleichmaßdehnung Ag ist Dehnung dieser Probe von Radius zu Radius bis zum Kraftmaximum.
- Totale Gleichmaßdehnung Agt
Wie Ag - jedoch einschließlich dem elastischen Anteil (der elastische Anteil zieht sich nach dem Bruch wieder zusammen)
Material ohne ausgeprägte Streckgrenze
Bei diesem Material handelt es sich entweder um einen Eisen-Werkstoff der einer weiteren Behandlung unterzogen wurde (Kaltumformung, Wärmebehandlung, etc.) oder um einen Stahl (Eisen mit zusätzlicher Legierung). Bei diesen Materialien ist die von Eisen bekannte Streckgrenze nicht mehr vorhanden bzw. legierter Stahl und andere Metalle (Aluminium, Bronze etc.) weisen keine Streckgrenze auf. Das Material wird bei einem Zugversuch stetig verlängert ohne dass es zu einem spontanen Kraftabfall (Spannungsabfall) kommt. Eine bleibende Verlängerung (Schädigung) des Materials ist also nicht so augenscheinlich erkennbar wie bei dem ersten Diagramm. Somit wurde in der Normung eine Ersatzstreckgrenze - die Dehngrenze als Möglichkeit zur Feststellung der ersten Schädigung definiert. Dabei wird beobachtet bei welcher Kraft bzw. Spannung das Material die Elastizität verlässt und bleibend verformt (gedehnt) wird. Als Vergleichsmaßstab wurde dazu allgemein festgelegt eine Verlängerung um 0,2 % bleibende Dehnung heranzuziehen.
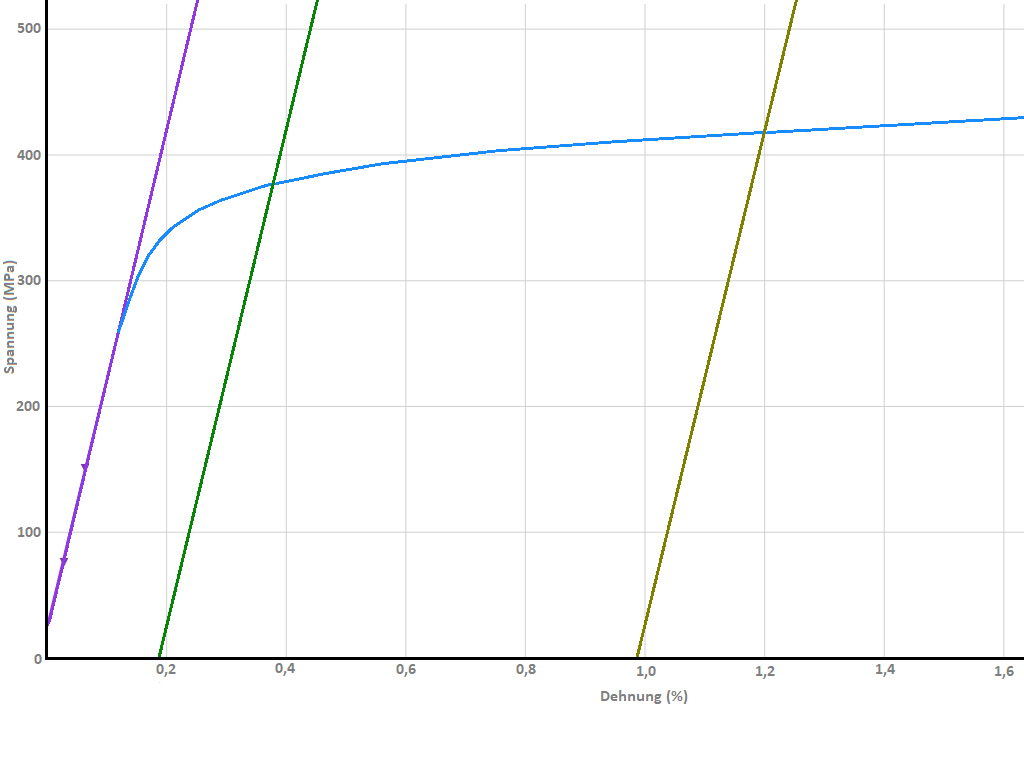
Hookesche-Gerade
Durch Robert Hook wurde erforscht, dass jeder Körper ein elastisches Verhalten aufweist. Verlängert man einen Körper um eine nicht zu hohe Länge so zieht sich dieser wieder zusammen. Am augenfälligsten ist dies bei Gummi oder einer Feder zu beobachten.
Elastizitätsmodul
Das Elastizitätsmodul ist die Errechnung des Material-Kennwertes des durch Hook endeckten Material-Elastizitätswertes. Am einfachsten ist diese Funktion zu erklären als Federkonstante des Materials. Zieht man eine Feder auseinander muss man für die Verlängerung einer Feder eine bestimmte Kraft pro mm verwenden. Z. B. braucht man dafür 100 N (ca. 10 kg) um die Feder 1 mm zu verlängern. Die Federkonstante C = 100 N /mm. Das E-Modul wird ähnlich berechnet. Jedoch werden die Kräfte durch Spannungen und die Längen durch Dehnungen ersetzt. Das so nominale E-Modul eines Materials z. B. Stahl (je nach Legierung z. B. 210.000 MPa) ergibt sich aus folgender theoretischer Berechnung: Könnte man die Ausgangslänge L0 verdoppeln ohne das der Stahl bleibend verlängert (geschädigt) wird (ohne das die Kurve horizontal abkippt) würde das Material eine Spannung erreichen von besagten 210.000 MPa. Dies ist sicher nicht möglich denn jeder Stahl würde bei einer Verlängerung um 100 % lange plastisch verformt und sicher auch brechen. Aber das E-Modul ist eben nur eine theoretische Zahl. Diese drückt letztlich die Steilheit der Hookeschen-Geraden (theoretischer Graphen) aus - die rote Linie im Diagramm. Das E-Modul muss bestimmt werden um zu dieser geraden Linie einen Versatz von 0,2 % (oder andere) auftragen zu können um dann an dem Schnittpunkt dieser parallelen Geraden die Spannung abgreifen zu können.
Dehngrenze Rp0,2
Spannungswert der ermittelt wird sobald die Probe um 0,2% Dehnung bleibend verlängert wurde. Dafür wird parallel zum E-Modul eine Gerade gebildet. An dem Kreuzungspunkt zum Graphen wir die Spannung bei 0,2 % Dehnung abgegriffen.
Dehngrenze Rp0.01
Wie Rp0,2 jedoch bei 0,01 % Verlängerung. Dies ist die kleinste übliche Dehngrenze und wird z. B. im Maschinenbau für statische Berechnungen genutzt. Eine Konstruktion darf nur so hoch belastet werden das dies niemals bleibend verformt wird. Also ist für die statische Berechnung ein noch kleinerer Kennwert der bleibenden Verformung von Interesse. Zur Auswertung wird parallel zum E-Modul eine Gerade gebildet. An dem Kreuzungspunkt zum Graphen wir die Spannung bei 0,01 % Dehnung abgegriffen.
Dehngrenze Rp1.0
Diese Dehngrenze ist weniger üblich. Sie entspricht der Spannung bei einer bleibenden Verlängerung der Probe um 1.0% Dehnung.
Vergleichbarkeit der Bruchdehnung
Im allgemeinen Sprachgebrauch bezieht sich Dehnung auf Erfahrungen und Beobachtungen unseres täglichen Lebens. Da wir dieses Phänomen nur an sehr elastischen, hochdehnfähigen Materialien beobachten können ist dieser Begriff mit einer Verlängerung belegt die sich auf Werkstoffe wie Gummi bezieht. Die Beobachtung verleitet dazu, dass sich alle Bereiche der (Gummi-) Zugprobe gleichmäßig verlängern bis zum Bruch. Man kann theoretisch einen Parallelstreifen oder Rundstab einer Zugbelastung aussetzen und zu jedem Zeitpunkt des Zugversuchs an jeder Stelle die gleiche Verlängerung abgreifen (Gleichmaßdehnung bis zum Bruch).
- Gummi bleibt bis zum Bruch komplett elastisch und zieht sich - solange es nicht gerissen ist - gänzlich zusammen bis auf die Ausgangslänge.
Metallverhält sich anders: Ist einmal eine Schädigungs-Schwelle überschritten kommt des (auch wenn noch keine Schädigung / Einschnürung zu sehen ist) zu einer bleibenden Verlängerung. Sobald die Probe zum Beispiel um 1 mm verlängert wurde zieht sich diese Verlängerung nur um 0,3 mm zusammen - 0,7 mm Verlängerung verbleibt.
- Zunächst verlängert sich eine Stahlprobe tatsächlich an allen Stellen (eines homogenen Querschnitts) gleichmäßig (Gleichmaßdehnung). Dieses Verhalten ändert sich jedoch dramatisch. Sobald alle Gefüge-Bestandteile bis zum Maximum verlängert wurden erfolgt das weitere Fließen nur noch partiell. Dort wo später der Bruch eintritt fließt das Material überproportional und es kommt zu einer Einschnürung (Taillenbildung). Im Bereich des späteren Bruchs kommt es zum Fließverhalten (Dehnung) wohingegen andere Bereiche nicht mehr verlängert werden.
- Dehnung ist Querschnitts- bzw. Volumenabhängig:
Am Beispiel von Luftballons wird dies deutlich:
Ein kleiner Luftballon kann bis zum Platzen nur gering aufgeblasen werden.
Ein großer Luftballon kann entsprechend größer aufgeblasen werden.
Stahl: Eine Probe mit einem großen Querschnitt besitzt im Inneren mehr Material zum Fließen als ein geringer Querschnitt. Daher kann eine Probe mit großem Querschnitt (bei gleicher Proben- bzw. Ausgangslänge) höher verlängert werden als eine Probe mit geringem Querschnitt:
Ein Rundstab Ø 10 mm kann von 100 mm auf 120 mm verlängert werden.
Ein Rundstab Ø 20 mm kann von 100 mm auf 125 mm verlängert werden (+ 5 mm).
Um die Bruchdehnung vergleichbar zu machen musste in die Dehnungsberechnung eine Systematik integriert werden um das differente Volumen zu berücksichtigen. Da Metall in Bezug auf das Volumen proportional fließt (mehr Volumen = höhere Verlängerung) wurde diese Gesetzmäßigkeit einbezogen. Die Bezugslänge Lo (Länge Null) wird also Querschnittsbezogen immer wieder neu berechnet indem der Proportionalitätsfaktor einbezogen wird. So wird also nicht mit einem starren Lo geprüft sondern die Länge Null (Lo ) wird berechnet unter Einbeziehung des Proportionalitätsfaktors K:
Lo = K x (Wurzel So)
K = Proportionalitätsfaktor 5,65
So = Probenquerschnitt in mm²
Berechnung des Lo (Ausgangslänge)
Rundprobe Ø 10 mm: Lo = 5,65 x (Wurzel(10 x 10 x 3,14 /4)) = ~ 50,06 ~ 50 mm
Rundprobe Ø 12 mm: Lo = 5,65 x (Wurzel(12 x 12 x 3,14 /4)) = ~ 60,07 ~ 60 mm
Neben dem Proportionalitätsfaktor K 5,65 gibt es noch den weniger gebräuchlichen Faktor 11,3.
Ein Tastarmdehnungsmesser bzw. Langwegdehnungsmesser vereinfacht die Prüfung bzw. Auswertung der Bruchdehnung: Dieser kontaktiert mit seinen Schneiden die Probe bei exakt diesem Maß (50,0 mm oder andere, nicht gerundete Zahlen) und verfolgt diese Anfangsmesslänge (Lo) bis zum Bruch. Die Berechnung kann dann auf einfache Weise erfolgen da nur Messwerte des Tastarmdehnungsmessers in die Messung einfließen.
Sofern kein (kostenintensiver) Langwegdehnungsmesser (Tastarmdehnungsmesser) verwendet wird muss die Probe vor dem Versuch markiert werden in einem Rasterabstand von 5 mm bzw. mit Körnerpunkten (die keinen vorzeitigen Bruch an dieser Stelle provozieren). Nach dem Bruch werden die Bruchstücke aneinandergelegt und die verlängerte Ausgangsmesslänge vermessen.
Besonderheiten bei dünnen Blechen
Sofern Bleche zu dünn sind kann aus der Dicke heraus kein Material fließen: Die Probe dehnt sich nicht proportional zum Querschnitt. Bei Blechen unter 3 mm Dicke wird daher die Dehnung an einer "nichtproportionalen Flachprobe" mit starrer Bezugslänge ermittelt. Bei Eisen- und Stahlblech erfolgt die Dehnungsberechnung auf Basis eines Ausgangslänge Lo von 80 mm (A80 Dehnung). Bei NE-Metallen erfolgt die Dehnungsberechnung auf Basis eines Lo von 50 mm (A50 Dehnung).
Dehnung ist nicht gleich Dehnung
Sofern das Ergebnis der Bruchdehnung keinen Index enthält (also nur Großbuchstabe A) muss man von einen Fließverhalten proportional zum Volumen ausgehen. In diesem Fall handelt es sich um die Bruchdehnung A(5,65).
Ist das Fließverhalten NICHT PROPORTIONAL muss dem Dehnungswert ein Index angefügt werden: Es handelt sich um eine nichtproportionale Flachprobe A80 oder A50 (bzw. das proportionale Fließverhalten A11,3)
Sofern Sie also Dehnungen vergleichen wolle müssen Sie (falls erforderlich) einen Index beachten. Falls die Dehnung unterschiedlicher Proben verglichen werden müssen diese umgerechnet werden. Dafür gibt es Berechnungsformeln bzw. wir haben eine Webseite geschaffen die die Dehnung in andere Dehnungsarten umrechnet.
Berechnung Bruchdehnung (Darstellung: Probenverlängerung in mm)
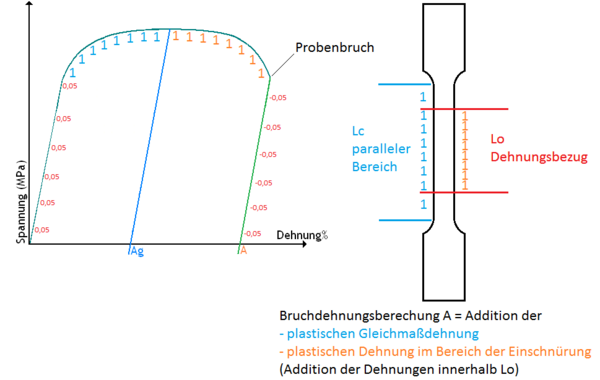
In der Grafik wird gezeigt warum die Bruchdehnung nicht über den Traversenweg gemessen werden kann: Die Dehnungswerte resultieren aus insgesamt 3 Bereichen:
- elastische Dehnung (Zahlen 0,05 mm), werden am Schluss abgezogen da sich die Probe nach dem Bruch um diesen Teil zusammenzieht
- plastische Dehnung im gesamten parallelen Bereich Lc (Gleichmaßdehnung Ag bis Fm)
- Fließdehnung im Bereich der Einschnürung - die Verlängerung erfolgt nur noch im Fließbereich
Nur die Zahlen im Lo-Bereich dürfen in die Bruchdehnungs-Berechnung einfließen!
Berechnung der Bruchdehnung
Aus unserer Erfahrung wissen wir, dass die Berechnung der Dehnung (Fließverhalten) von Metallen / einer Zugprobe der am schwierigsten zu erklärende Kennwerte ist. Metalle weisen nämlich eine Besonderheit bei der Dehnung auf. Ein jeder von uns hat schon einmal beobachtet, wie Metall in eine bleibende Verformung gebracht wird: Biegt man ein Blech nur ein wenig so federt dieses wieder zurück in die Ausgangsform (Elastizitäts-Verhalten). Biegt man aber immer weiter so ist irgendwann der Punkt erreicht bei dem dieses Stück Metall gekrümmt bleibt: Es ist bleibend verformt. Ähnlich dem elastischen / plastischen Biegen eines Stahls verhält sich dieser auch unter Zugbelastung. Verlängert man diesen Stahl nur gering so zieht sich dieser wieder zusammen (ähnlich Gummi). Erst wenn man die Schädigungsgrenze überschreitet verlängert sich der Stahl bleibend. Für bestimmte Aufgaben ist es in der Industrie wichtig das Dehnverhalten eines Metalls exakt zu bestimmen. Denn nur wenn man das Umformverhalten (Dehnfähigkeit) exakt kennt kann man sicherstellen, dass das Metall in die gewünschte Form gebracht werden kann ohne dass eine zu große Schädigung (vorzeitiger Bruch) erfolgt. Logisch wird dies wenn man einmal nachvollzieht, dass aus einer planen Blechplatte durch extreme Umformung ein Kochtopf entsteht - ein Tiefziehvorgang mit extremen Dehnungen.
Metall dehnt sich bis zum Bruch aber nicht an allen Stellen gleichmäßig. Sobald die Gleichmaßdehnung beim Kraftmaximum überschritten ist fließt das Material an der schwächsten Stelle immer extremer (und nur noch dort), schnürt sich ein (Taillenbildung) und bricht dort. Da das Fließverhalten des Metalls nicht an allen Stellen gleich ist muss also eine Systematik gefunden werden um die Dehnung vergleichbar bestimmen zu können. Daher wird die Dehnung A (Bruchdehnung) ausschließlich auf eine exakt definierte, aber variable Stecke bezogen. Dieses Bezugsmaß (Länge null - kurz L0) wird als Grundlage der Berechnung herangezogen und mit der Formel berechnet.
Hinweis: Die Dehnung kann nicht direkt miteinander Verglichen werden. Eine Dehnung A (A5,65) unterscheidet sich von einer Dehnung A80 / A11,3 / A50 / A100 / A200 erheblich. Zum Vergleich der Dehnungen kann man diese umrechnen.
A Bruchdehnung (in %)
L0 Anfangsmesslänge der Probe (Ausgangslänge)
Lu Länge nach dem Bruch (beinhaltet Anfangsmesslänge L0 und die Verlängerung dieses Teils)
Formel zur Berechnung der Bruchdehnung A für einen Zugversuch
(Anmerkung: Wird der Kurzbuchstabe A ohne Index verwendet handelt es sich um die Dehnung A5,65)
Formel: A = ((Lu – L0)/L0)x 100 bzw.:
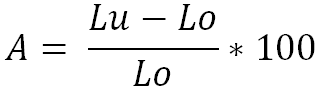
Begriffserklärung der Zugprüfung bei Metallen
Kurzzeichen | Einheit | Benennung / vereinfachte Erklärung |
a0 | mm | Anfangsdicke einer Flachprobe oder Wanddicke eines Rohres zu Beginn des Zugversuchs |
b0 | mm | Breite einer Flachprobe in der Versuchslänge | mittlere Breite einer Rohrstreifenprobe | Profildraht zu Beginn des Zugversuchs |
D0 | mm | Außendurchmesser eines Rohres |
L0 | mm | Ausgangsmesslänge (Bezugslänge bzw. Anfangslänge für die Dehnung) |
LC | mm | Versuchslänge (paralleler Teil der Messlänge zwischen den Radien) |
Lt | mm | Gesamtlänge der Probe einschließlich Köpfen |
LU | mm | Messlänge nach dem Bruch (L0 gedehnt) |
S0 | mm² | Anfangsquerschnitt der Probe: Dicke x Breite | Durchmesser | Rohrdurchmesser x Wandstärke | Gewichtsmethode: Gewicht / Länge / Dichte |
SU | mm² | kleinster Querschnitt nach dem Bruch (zur Berechnung der Einschnürung - Fließverhalten / Dehnungsverhalten im Querschnitt ) |
K | - | Proportionalitätsfaktor - Verhältnis des Querschnitts zu L0 (5,65 oder 11,3) |
Z | % | Brucheinschnürung - Verhältnis zwischen S0 und SU (Berechnung der Einschnürung - Fließverhalten / Dehnungsverhalten im Querschnitt |
R (σ) | MPa | Spannung - Kraft geteilt durch den Anfangsprobenquerschnitt |
A | % | Bruchdehnung - Verlängerung der Probe bezogen auf die Ausgangsmesslänge L0 (ohne Index = Dehnung A5,65) |
At | % | wie A, jedoch beinhaltet dieser Wert auch die (totale) Dehnung inkl. elastischer Anteil |
Ag | % | Gleichmaßdehnung: Die Dehnung von Metallen erfolgt bis zum Kraftmaximum (Fm Force Maximum) bzw. Spannungs-Maximum (Rm) |
Agt | % | wie Ag, jedoch beinhaltet dieser Wert die elastische Dehnung |
A5,65 | % | typischer Proportionalitätsfaktor zur Berechnung des L0 (nicht für Flachproben Dicke <3,0 mm | Drähte Ø <4 mm anwendbar) |
A11,3 | % | Proportionalitätsfaktor zur Berechnung des L0 (nicht für Flachzugproben Dicke <3,0 mm | Drähte Ø <4 mm anwendbar) Anmerkung: Dehnungswerte sind miteinander nicht direkt vergleichbar - bitte nutzen Sie zur Umrechnung unseren Kalkulator. |
A50 | % | Bruchdehnung von Flachzugproben aus Blech mit einer Dicke 0,1 - 3,0 mm (üblichste Probenform bei NE- Metalle wie Alu, Kupfer |
A80 | % | Bruchdehnung von Flachzugproben aus Blech mit einer Dicke 0.1 - 3.0 mm (üblichste Probenform bei Stahl-Flachzugproben |
A100 | % | Bruchdehnung von Drähten: Bei Drähten erfolgt der Bruch oft an undefinierter Stelle. Würde man eine A5,65 Dehnung |
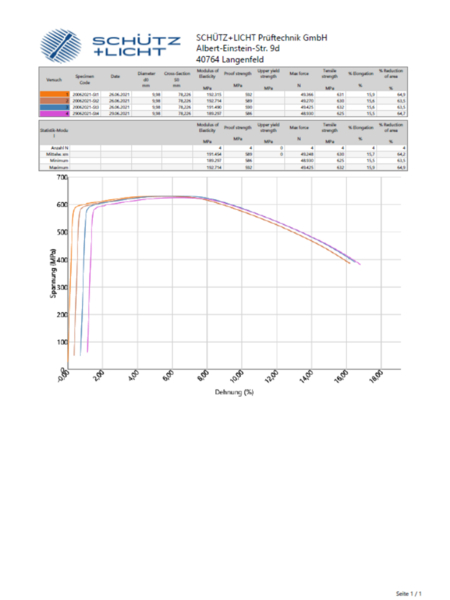
Prüfbericht (Prüfzeugnis)
Inhaltliche Wiedergabe der ISO 6892-1 in Bezug auf einen Prüfbericht (siehe auch die weiter unten: PDF-Download Prüfbericht) Die ISO 6892-1 aus 2017-02 schreibt vor das der Prüfbericht folgende Informationen enthalten muss (Ausnahme: Die Parteien vereinbaren etwas anderes) | |
| 1. Hinweis auf die Norm ISO 6892 und die Prüfgeschwindigkeit - hier: A224 | A2XX = 0.00025 mm/mm/Sekunde (Führungsgröße Extensometer) AX2X = 0.00025 mm/mm/Sekunde (Führungsgröße Traversenweg bezogen auf Lc) AXX4 = 0.0067 mm/mm/Sekunde (Führungsgröße Traversenweg bezogen auf Lc) |
| 2. Kennzeichnung der Probe | Probennummer für Rückführbarkeit |
| 3. Werkstoff, falls bekannt | ST370 - Baustahl |
| 4. Art der Probe | Flachprobe |
| 5. Probenlage und -richtung | Entnahme: 50 mm von der Bandkante. Querprobe |
| 6. Versuchs-Regelungsarten + Geschwindigkeiten | nur falls Abweichen, siehe auch 1. |
| 7. Prüfergebnisse | Reh, Rp0,2, Rm, Ag, A80 (E-Modul ist KEIN Ergebnis nach ISO6892-1 dient aber als Gutbefund der Versuche Werte gerundet R-Werte ohne Nachkommastelle auf nächste ganze Zahl A-Werte mit Rundung auf 0,5% Z-Brucheinschnürung auf 1% gerundet (falls relevant) |